دایره محاطی و محیطی در مثلث و بیضی و مارپیچ

دایره محاطی و محیطی در مثلث و بیضی و مارپیچ

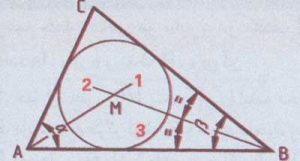
رسم دایره محاطی یک مثلث :

داده ها : مثلث

1. زاویه آلفا را نصف کنید.

2. زاویه بتا را نصف کنید.

3. نیمساز زاوی ها را ادامه داده تا همدیگر را قطع نمایند. نقطه M مرکز دایره محاطی است.

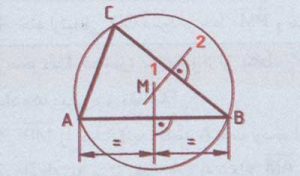
رسم دایره محیطی یک مثلث :

1. عمود منصف ضلع AB را رسم نمایید.

2. عمود منصف ضلع CD را رسم نمایید.

3. عمود منصف اضلاع را ادامه داده تا همدیگر را قطع نمایند ، نقطه M مرکز دایره محاطی است.

رسم بیضی :

داده ها : محورهای  AB و CD

1. دو دایره به مرکز نقطه M و به قطرهای  AB و CD  رسم نمایید.

2. از نقطه M چندین پاره خط رسم نمایید تا هر دو دایره را قطع کند ( E و F )

3. از نقاط به دست آمده خطوطی به موازات محور AB و CD  رسم نمایید.

4. نقاط به دست آمده را به هم وصل کنید.

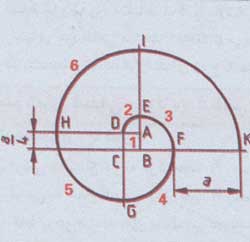
رسم مارپیچ یا مارپیچ چند مرکزه ( رسم تقریبی با پرگار ) :

داده ها : گام a

1. مربع ABCD  را به اندازه ضلع a/4 رسم کنید.

2. ربع دایره به شعاع AD  به مرکز A و نقطه E را نتیجه می دهد.

3. ربع دایره به شعاع BE به مرکز B  و نقطه F  را نتیجه می دهد.

4.ربع دایره به شعاع CF به مرکز C و نقطه G را نتیجه می دهد.

5.ربع دایره به شعاع DG به مرکز D و نقطه H را نتیجه می دهد.

6.ربع دایره به شعاع AH به مرکز A و نقطه I را نتیجه می دهد.

یک مثلث همواره دارای یک رشته است که مرکز آن (مرکز) نقطه همبستگی bisectors زاویه است.

یک چند ضلعی که یک حلقه نامیده می شود، یک چند ضلعی محدود یا چند ضلعی مماس نامیده

می شود و گفته می شود قابل inscribable است.

دایره محاطی و محیطی در مثلث و بیضی و مارپیچ